Algorithm

LRU和LRU-K

August 12, 2019
LRU, LRU-K, Caching, Algorithm

缓存淘汰机制 #

缓存淘汰机制在缓存需要被清理的时候使用。主要有以下几种算法：

  • FIFO：先入先出，优先清理最先被缓存的数据对象。实现简单，直接使用队列就可以实现。
  • LRU：最近最久未被使用，优先清理最近没有被使用的对象。使用一个最近使用时间降序的有序队列，优先清理队列对后的数据。与LFU的区别在于：LRU是按照最近使用使用的时间排序，LFU需要维护一个使用频次并用于排序。
  • LFU：最近最少使用，优先清理最近最少使用的数据对象。使用一个使用次数降序的有序队列，优先清理队列最后的数据。

// 其中LRU和LFU可以通过维护一个Hashmap来提高访问效率。

LRU / LRU-1 #

LRU（Least recently used，最近最少使用）算法根据数据的历史访问记录来进行淘汰数据，其核心思想是“如果数据最近被访问过，那么将来被访问的几率也更高”。实现思路也很简单，就不过多赘述了：

// data to cache
type data struct {
    key   int
    value int
}

// LRUCache structture to support LRU alg.
type LRUCache struct {
    recoder map[int]*list.Element // key hit for get op O(1)
    linked  *list.List            // linked-list
    rest    int                   // rest capacity
}

// Constructor ... to generate a LRUCache
func Constructor(capacity int) LRUCache {
    c := LRUCache{
        rest:    capacity,
        linked:  list.New(),
        recoder: make(map[int]*list.Element),
    }

    return c
}

// Get ... O(1) wanted
func (c *LRUCache) Get(key int) int {
    v, ok := c.recoder[key]
    if !ok {
        return -1
    }
    // hit the key
    _ = c.linked.Remove(v)
    c.recoder[key] = c.linked.PushFront(v.Value)
    fmt.Println("get", key, c.linked.Len(), c.recoder)

    return v.Value.(*data).value
}

// Put ... O(1) wanted
func (c *LRUCache) Put(key int, value int) {
    if v, ok := c.recoder[key]; ok {
        c.linked.Remove(v)
        goto h
    }

    if c.rest == 0 {
        tail := c.linked.Back()
        c.linked.Remove(tail)
        delete(c.recoder, tail.Value.(*data).key)
    } else {
        c.rest--
    }
h:
    head := c.linked.PushFront(&data{key, value})
    c.recoder[key] = head
}

LRU-K #

LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题，其核心思想是将“最近使用过1次”的判断标准扩展为“最近使用过K次”。也就是说没有到达K次访问的数据并不会被缓存，这也意味着需要对于缓存数据的访问次数进行计数，并且访问记录不能无限记录，也需要使用替换算法进行替换。当需要淘汰数据时，LRU-K会淘汰第K次访问时间距当前时间最大的数据。

...

Stack实现O(1)的Min和Max：从空间换时间到数学魔法的探究

March 1, 2018
Algorithm
Golang, Algorithm

栈（Stack）作为一种基础的数据结构，其 Push 和 Pop 操作的 $O(1)$ 时间复杂度通过栈顶指针即可轻松保证。但如果在实际业务场景或算法挑战中，要求我们实现 O(1) 时间复杂度内的 Min 和 Max 操作，问题就变得有趣起来了。

背景 #

在常规的栈实现中，如果我们需要获取栈内的最大值或最小值，通常的做法是遍历整个栈。这种做法的时间复杂度是 $O(N)$，其中 $N$ 是栈中元素的数量。

然而，在某些对性能要求苛刻的场景（如实时流监控窗口的最值计算）或者算法面试中，通常会要求我们将 Min 和 Max 的获取时间也压缩到 $O(1)$。

面对这个需求，我们最先想到的思路通常是“空间换时间”：即通过维护额外的状态来实时记录最值。那么，具体该如何设计并保证数据的一致性呢？

方案一：辅助栈 (Auxiliary Stack) #

最直观的思路是设置一个辅助结构来同步记录最值。我们以“最大值”为例，引入一个辅助栈 SMax。

算法描述 # 

State:
  DataStack: [Integer] // The primary storage
  SMax:      [Integer] // Auxiliary stack to store the sequence of maximums

在这个方案中，逻辑如下：

  • Push: 当元素入栈时，我们不仅将其压入数据栈；同时，比较该元素与 SMax 栈顶元素。如果该元素大于等于 SMax 栈顶元素（或者 SMax 为空），则将该元素也压入 SMax。
  • Pop: 当元素出栈时，判断该元素是否等于 SMax 的栈顶元素。如果相等，说明我们要弹出的正是当前的最大值，因此 SMax 也要同步弹出栈顶。

伪代码描述 # 

Function Push(element):
    DataStack.Push(element)
    // If element is new max, push to SMax
    IF SMax.IsEmpty() OR element >= SMax.Top():
        SMax.Push(element)

Function Pop():
    value = DataStack.Pop()
    // If we are popping the current max, pop from SMax too
    IF value == SMax.Top():
        SMax.Pop()
    RETURN value

Function GetMax():
    RETURN SMax.Top()

场景推演 #

为了验证这个逻辑，我们以序列 1, 3, 6, 1, 12, 512, 12, 5121, 121, 412 为例进行推演：

...

Trie树学习

February 11, 2018
Algorithm
Algorithm, Trie

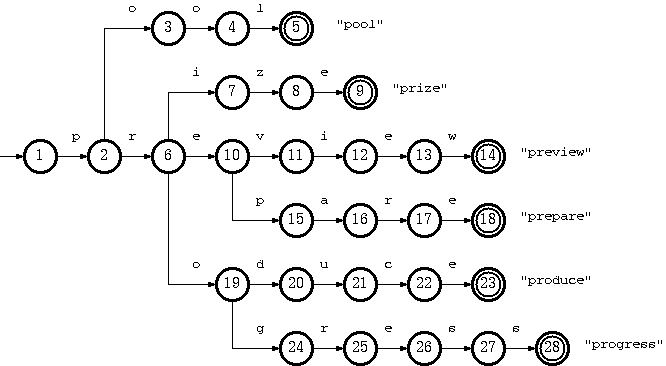
Trie树(Retrieval Tree)又称前缀树，可以用来保存多个字符串，并且查找效率高。在trie中查找一个字符串的时间只取决于组成该串的字符数，与树的节点数无关。Trie树形状如下图： Trie树

应用场景 #

  • 词频统计（搜索引擎常用）
  • 前缀单词搜索

构造Trie树 #

构造Trie树有如下几种方式（非全部）：

// 结构1，简单且直观，但是空间闲置较多，利用率低下
type TrieNode struct{
	Char	 rune
	Children [27]*TrieNode
}

// 结构二 可变数组Trie树, 减少了闲置指针，但是只能通过遍历来获取下一状态，降低了查询效率
type TrieNode struct {
	Char rune
	Children []*TrieNode
}

// 结构3，双数组Trie树，空间和时间上耗费较为均衡，但是动态构建，解决冲突耗费时间较多
type TrieNode struct {
	Base  []int
	Check []int
}

数组构造方式 #

这里选择双数组方式来实现Trie树。

基于数组的实现方式，把trie看作一个DFA，树的每个节点对应一个DFA状态，每条从父节点指向子节点的有向边对应一个DFA变换。遍历从根节点开始，字符串的每个字符作为输入用来确定下一个状态，直到叶节点。 —- 摘自参考资料，Trie数组实现原理

数组Trie之DFA

关于双数组：

  • Base数组，表示后即节点的基地址的数组，叶子节点没有后继
  • Check数组，用于检查

Trie树应用之前缀搜索 #

前缀搜索。也就是给一定的字符串，给出所有以该字符串开始的单词。譬如，Search(“go”)，得到[“go”, “golang”, “google”, …]

三种构造方式的优劣分析 #

Trie树（数组Trie树） #

每个节点都含有26个字母指针，但并不是都会使用，内存利用率低。时间复杂度：O(k)， 空间复杂度：O(26^n)

...

动态规划之字符串编辑距离

February 11, 2018
Algorithm
Algorithm, Dynamic Programming, Levenshtein Distance

问题描述 #

给定 2 个字符串 a, b. 编辑距离是将 a 转换为 b 的最少操作次数，操作只允许如下 3 种： 插入一个字符，例如：fj -> fxj 删除一个字符，例如：fxj -> fj 替换一个字符，例如：jyj -> fyj

函数原型：

func LevenshteinDis(str1, str2 string) int {
    ...
}

算法适用场景 #

  • 拼写检查
  • 输入联想
  • 语音识别
  • 论文检查
  • DNA分析

问题分析 #

假定函数edit_dis(stra, strb)表示，stra到strb的编辑距离。算法问题可以分为四种情况：

  1. edit_dis(0, 0) = 0
  2. edit_dis(0, strb) = len(strb)
  3. edit_dis(stra, strb) = len(stra)
  4. edit_dis(stra, strb) = ?

对于4th一般情况，没有办法直接给出求解方式，我们来分析edit_dis(stra+chara, strb+charb)可能的情况：

  1. stra能转成strb，那么只需要判断chara是不是等于charb (cur_cost = 0 if chara == charb else 1)
  2. stra+chara能转成strb, 那么要让stra + chara 转成strb+ charb, 只需要插入charb就行了
  3. 如果stra 可以直接转成strb+charb，那么删除chara就可以转换成功了

综上的分析，可以得到如下DP公式：

...

访问量 访客数