Algorithm

介绍一下snowflake和rc4

April 5, 2019
Algorithm
Golang, Tools, Crypto, RC4, Snowflake

snowflake是twitter公司开源的生成唯一ID的网络服务，具有很强的伸缩性，这里只取用生成唯一ID的算法部分。 rc4（Rivest Cipher 4）是一种流加密算法，密钥长度可变，它的加解密使用相同的密钥，因此也属于对称加密算法。

为啥要介绍这两种算法？ #

其一，snowflake可以生成唯一ID，而相比与UUID，snowflake生成的ID更加“好用”，这个放在后面解释。 其二，UUID和snowflake虽然可以生成唯一ID，但是无法适用于所有场景，譬如说“生成推广码”。生成推广码的时候，希望尽可能短而精，很明显唯一ID都不太短。

snowflake #

snowflake的唯一ID是一个64bit的int型数据，相较于UUID来说耗费空间更小，可以更方便的作为数据库主键来索引和排序。

snowflake

生成过程： #
  • 置0不用
  • timestamp（41bits）精确到ms。
  • machine-id（10bits）该部分其实由datacenterId和workerId两部分组成，这两部分是在配置文件中指明的。datacenterId（5bits）方便搭建多个生成uid的service，并保证uid不重复。workerId（5bits）是实际server机器的代号，最大到32，同一个datacenter下的workerId是不能重复的。
  • sequence-id(12bits)，该id可以表示4096个数字，它是在time相同的情况下，递增该值直到为0，即一个循环结束，此时便只能等到下一个ms到来，一般情况下4096/ms的请求是不太可能出现的，所以足够使用了。
优势和缺陷： #
  • 速度快，无依赖，原理和实现简单，也可以根据自己的需求做算法调整
  • 依赖机器时间，如果时间回拨可能导致重复的ID

rc4 #

RC4加密算法也是一种基于密钥流的加密算法。

首先，rc4根据明文和密钥生成的密钥流，其长度和明文的长度是相等的，也就是说明文的长度是500字节，那么密钥流也是500字节，这也是我们用来生成推广码的原因之一了；其次，rc4是是对称加密完全可以通过密文得到明文，也就是说在生成码的时候把必要信息放在明文中，在使用密文的时候可以不用查库也能得到相关的信息，譬如用户ID，这是原因之二。

使用场景 #

现在需要生成一种码，短小易记，且唯一，但并不需要大量。

上述的snowflake和UUID都很容易实现唯一，但是短小就不符合要求了。因为并不需要大量生成这种码，因此我们考虑用自增ID + RC4来实现：

package main

import (
	"crypto/rc4"
	"encoding/hex"
	"fmt"
	"log"
)

func main() {
	cipher, err := rc4.NewCipher([]byte("thisiskey"))
	if err != nil {
		log.Fatalf("wrong with NewCipher: %v", err)
	}

	c := map[string]bool{}
	for i := 0; i < 1000; i++ {
		src := []byte(fmt.Sprintf("%7d", i))
		dst := make([]byte, len(src))
		cipher.XORKeyStream(dst, src)
		s := toString(dst) // 密文是不可读的字节流，这里采用hex编码
		println(s)         // 形如：a09def6b6e4797
		c[s] = true
	}

	println(len(c)) # 1000
}

func toString(src []byte) string {
	return hex.EncodeToString(src)
}

参考 #

Stack实现O(1)的Min和Max：从空间换时间到数学魔法的探究

March 1, 2018
Algorithm
Golang, Algorithm

栈（Stack）作为一种基础的数据结构，其 Push 和 Pop 操作的 $O(1)$ 时间复杂度通过栈顶指针即可轻松保证。但如果在实际业务场景或算法挑战中，要求我们实现 O(1) 时间复杂度内的 Min 和 Max 操作，问题就变得有趣起来了。

背景 #

在常规的栈实现中，如果我们需要获取栈内的最大值或最小值，通常的做法是遍历整个栈。这种做法的时间复杂度是 $O(N)$，其中 $N$ 是栈中元素的数量。

然而，在某些对性能要求苛刻的场景（如实时流监控窗口的最值计算）或者算法面试中，通常会要求我们将 Min 和 Max 的获取时间也压缩到 $O(1)$。

面对这个需求，我们最先想到的思路通常是“空间换时间”：即通过维护额外的状态来实时记录最值。那么，具体该如何设计并保证数据的一致性呢？

方案一：辅助栈 (Auxiliary Stack) #

最直观的思路是设置一个辅助结构来同步记录最值。我们以“最大值”为例，引入一个辅助栈 SMax。

算法描述 # 

State:
  DataStack: [Integer] // The primary storage
  SMax:      [Integer] // Auxiliary stack to store the sequence of maximums

在这个方案中，逻辑如下：

  • Push: 当元素入栈时，我们不仅将其压入数据栈；同时，比较该元素与 SMax 栈顶元素。如果该元素大于等于 SMax 栈顶元素（或者 SMax 为空），则将该元素也压入 SMax。
  • Pop: 当元素出栈时，判断该元素是否等于 SMax 的栈顶元素。如果相等，说明我们要弹出的正是当前的最大值，因此 SMax 也要同步弹出栈顶。

伪代码描述 # 

Function Push(element):
    DataStack.Push(element)
    // If element is new max, push to SMax
    IF SMax.IsEmpty() OR element >= SMax.Top():
        SMax.Push(element)

Function Pop():
    value = DataStack.Pop()
    // If we are popping the current max, pop from SMax too
    IF value == SMax.Top():
        SMax.Pop()
    RETURN value

Function GetMax():
    RETURN SMax.Top()

场景推演 #

为了验证这个逻辑，我们以序列 1, 3, 6, 1, 12, 512, 12, 5121, 121, 412 为例进行推演：

...

Trie树学习

February 11, 2018
Algorithm
Algorithm, Trie

Trie树(Retrieval Tree)又称前缀树，可以用来保存多个字符串，并且查找效率高。在trie中查找一个字符串的时间只取决于组成该串的字符数，与树的节点数无关。Trie树形状如下图： Trie树

应用场景 #

  • 词频统计（搜索引擎常用）
  • 前缀单词搜索

构造Trie树 #

构造Trie树有如下几种方式（非全部）：

// 结构1，简单且直观，但是空间闲置较多，利用率低下
type TrieNode struct{
	Char	 rune
	Children [27]*TrieNode
}

// 结构二 可变数组Trie树, 减少了闲置指针，但是只能通过遍历来获取下一状态，降低了查询效率
type TrieNode struct {
	Char rune
	Children []*TrieNode
}

// 结构3，双数组Trie树，空间和时间上耗费较为均衡，但是动态构建，解决冲突耗费时间较多
type TrieNode struct {
	Base  []int
	Check []int
}

数组构造方式 #

这里选择双数组方式来实现Trie树。

基于数组的实现方式，把trie看作一个DFA，树的每个节点对应一个DFA状态，每条从父节点指向子节点的有向边对应一个DFA变换。遍历从根节点开始，字符串的每个字符作为输入用来确定下一个状态，直到叶节点。 —- 摘自参考资料，Trie数组实现原理

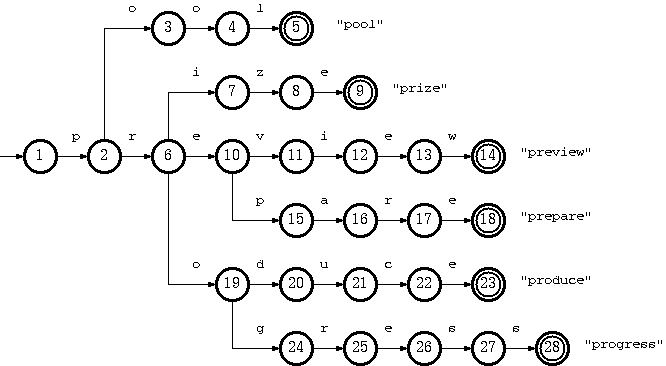
数组Trie之DFA

关于双数组：

  • Base数组，表示后即节点的基地址的数组，叶子节点没有后继
  • Check数组，用于检查

Trie树应用之前缀搜索 #

前缀搜索。也就是给一定的字符串，给出所有以该字符串开始的单词。譬如，Search(“go”)，得到[“go”, “golang”, “google”, …]

三种构造方式的优劣分析 #

Trie树（数组Trie树） #

每个节点都含有26个字母指针，但并不是都会使用，内存利用率低。时间复杂度：O(k)， 空间复杂度：O(26^n)

...

动态规划之字符串编辑距离

February 11, 2018
Algorithm
Algorithm, Dynamic Programming, Levenshtein Distance

问题描述 #

给定 2 个字符串 a, b. 编辑距离是将 a 转换为 b 的最少操作次数，操作只允许如下 3 种： 插入一个字符，例如：fj -> fxj 删除一个字符，例如：fxj -> fj 替换一个字符，例如：jyj -> fyj

函数原型：

func LevenshteinDis(str1, str2 string) int {
    ...
}

算法适用场景 #

  • 拼写检查
  • 输入联想
  • 语音识别
  • 论文检查
  • DNA分析

问题分析 #

假定函数edit_dis(stra, strb)表示，stra到strb的编辑距离。算法问题可以分为四种情况：

  1. edit_dis(0, 0) = 0
  2. edit_dis(0, strb) = len(strb)
  3. edit_dis(stra, strb) = len(stra)
  4. edit_dis(stra, strb) = ?

对于4th一般情况，没有办法直接给出求解方式，我们来分析edit_dis(stra+chara, strb+charb)可能的情况：

  1. stra能转成strb，那么只需要判断chara是不是等于charb (cur_cost = 0 if chara == charb else 1)
  2. stra+chara能转成strb, 那么要让stra + chara 转成strb+ charb, 只需要插入charb就行了
  3. 如果stra 可以直接转成strb+charb，那么删除chara就可以转换成功了

综上的分析，可以得到如下DP公式：

...

访问量 访客数