Trie树(Retrieval Tree)又称前缀树,可以用来保存多个字符串,并且查找效率高。在trie中查找一个字符串的时间只取决于组成该串的字符数,与树的节点数无关。Trie树形状如下图:

应用场景 #
- 词频统计(搜索引擎常用)
- 前缀单词搜索
构造Trie树 #
构造Trie树有如下几种方式(非全部):
// 结构1,简单且直观,但是空间闲置较多,利用率低下
type TrieNode struct{
Char rune
Children [27]*TrieNode
}
// 结构二 可变数组Trie树, 减少了闲置指针,但是只能通过遍历来获取下一状态,降低了查询效率
type TrieNode struct {
Char rune
Children []*TrieNode
}
// 结构3,双数组Trie树,空间和时间上耗费较为均衡,但是动态构建,解决冲突耗费时间较多
type TrieNode struct {
Base []int
Check []int
}
数组构造方式 #
这里选择双数组方式来实现Trie树。
基于数组的实现方式,把trie看作一个DFA,树的每个节点对应一个DFA状态,每条从父节点指向子节点的有向边对应一个DFA变换。遍历从根节点开始,字符串的每个字符作为输入用来确定下一个状态,直到叶节点。 —- 摘自参考资料,Trie数组实现原理
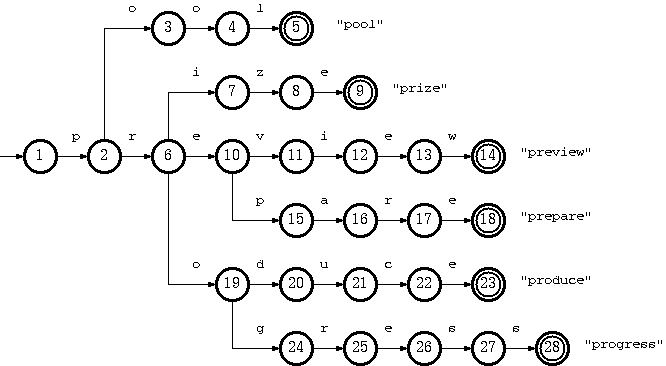
关于双数组:
- Base数组,表示后即节点的基地址的数组,叶子节点没有后继
- Check数组,用于检查
Trie树应用之前缀搜索 #
前缀搜索。也就是给一定的字符串,给出所有以该字符串开始的单词。譬如,Search(“go”),得到[“go”, “golang”, “google”, …]
三种构造方式的优劣分析 #
Trie树(数组Trie树) #
每个节点都含有26个字母指针,但并不是都会使用,内存利用率低。时间复杂度:O(k), 空间复杂度:O(26^n)
双数组Trie树 #
构造调整过程中,每个状态都依赖于其他状态,所以当在词典中插入或删除词语的时候,往往需要对双数组结构进行全局调整,灵活性能较差。双数组已经大幅改善了经典Trie树的空间浪费,但是冲突发生的时候,总是往后寻址,不可避免数组空置。随着数据量增大,冲突的几率也越来越大,字典树的构建也越来越慢。如果核心词典已经预先建立好并且有序的,并且不会添加或删除新词,那么这个缺点是可以忽略的。所以常用双数组Tire树都是载入整个预先建立好的核心分词词典。
Tail-Trie树 #
三数组Trie树实在双数组的基础上优化而来,增加了tail节点,就是将非公共前缀的词尾合并成为一个节点,减少节点总数,提升词典树的构建速度。如图:
